Algebra can sometimes seem like a different language, with its numbers and letters jumbled together in cryptic ways. But don’t fret! With the right approach, it can become as natural as any other subject. Whether you’re just diving into algebraic concepts in Grade 6 or refining your skills in Grade 12, having a clear understanding will open doors to more complex math and real-world applications with or without a Math tutor online.
This blog is here to help Canadian students navigate the world of algebra with confidence.
1. The Building Blocks of Algebra
Algebra serves as a cornerstone for more advanced math topics and plays a crucial role in various real-world applications. To demystify algebra, it’s essential to understand its foundational concepts.
Expressions and Variables:
In algebra, a combination of numbers and letters that doesn’t contain an equals (=) sign is known as an expression. For instance, 3x + 7 or y – 5 are expressions. The letters (‘x’, ‘y’ etc.) are called variables, representing unknown values.

Equations:
An equation is a statement asserting the equality of two expressions, meaning they represent the same value. For example:
4 + x = 9
In this equation, to find the value of x, you’d subtract 4 from both sides, yielding x = 5.
2y = 14
Here, to determine ‘y’, you’d divide both sides by 2, which means y = 7.
Multiple Variables:
Sometimes equations involve more than one variable:
x + y = 12
Without additional information, this equation has multiple solutions. For example, if x=7, then y=5. But if x=2, then y=10. This is a linear equation in two variables.
Quadratic Equations:
These are polynomial equations of the second degree. A common form is:
ax^2 + bx + c = 0
For example:
x^2 – 5x + 6 = 0
This equation can be factored as (x-2)(x-3) = 0. Hence, x could be 2 or 3.
Real-life Application:
Imagine you are splitting the bill at a restaurant. You ordered items for a total cost of $x, and your friend’s total is $y. If you both share the bill equally, and each person contributes $30, it means x + y = 60.
With a deeper understanding of these basic components and consistent practice, algebraic problems become more approachable. And remember, whenever in doubt, sketching, using real-world contexts, or seeking help from peers or best Math tutors online can make the process even more manageable.
2. Importance of Algebra in Real Life
Algebra isn’t just a set of arbitrary rules and techniques to torment students—it’s a powerful tool that has countless applications in our daily lives and various professions. Let’s delve into some real-world examples that illuminate algebra’s significance:
Budgeting & Finance:
Suppose you’re planning to save up for a new gadget that costs $y. If you put away $x each month, you can determine the number of months it’ll take to afford the gadget with the equation y/x. For example, if the gadget costs $300 and you save $50 monthly, you’ll need to save for 6 months.

Cooking:
Scaling recipes up or down involves algebra. If a recipe serves 4 and you need it for 10, an algebraic ratio can help adjust the ingredients proportionally.
Home Projects:
Say you’re painting a room. If a can of paint covers an area ‘a’ and your room’s total surface area to be painted is ‘b’, you can use algebra to determine how many paint cans you’ll need, given by b/a.
Technology:
Modern technologies, like GPS and search engines, use complex algebraic algorithms to determine the quickest route or the most relevant search results.
Health & Medicine:
Pharmacists use algebra to determine the correct dosage of medicine based on a patient’s weight and age.
Business & Economics:
Suppose a company determines that their profit P is given by the equation P = 5x – 10, where x is the number of items sold. This equation helps the business understand how selling more items will affect their profit.
Engineering & Architecture:
Building bridges, roads, or skyscrapers? Engineers and architects utilize algebraic equations to ensure structures are safe and robust. For instance, understanding the load a bridge can bear involves solving equations.
Environmental Science:
Predicting changes in ecosystems or understanding the growth of populations can be described using algebraic models.
Travel:
If you’re driving to a destination 300 kilometres away and you travel at a consistent speed of 75 kilometers per hour, algebra can determine the time it’ll take. By using the formula: Time = Distance/Speed, it’ll take 4 hours to reach.
These examples underscore the fact that algebra is intertwined with so many aspects of our lives. It equips us with the skills to solve problems, make informed decisions, and understand the world’s intricacies. So the next time you’re confronted with an algebraic problem, remember—it’s not just about ‘x’s and ‘y’s; it’s about navigating life’s challenges with precision and clarity.
3. Approaching Equations and Formulas
Every math challenge, no matter how daunting, can be tackled with a structured approach. Algebra is no exception. Here’s a more detailed, step-by-step breakdown to guide you through solving algebraic problems, ensuring you retain clarity and precision:
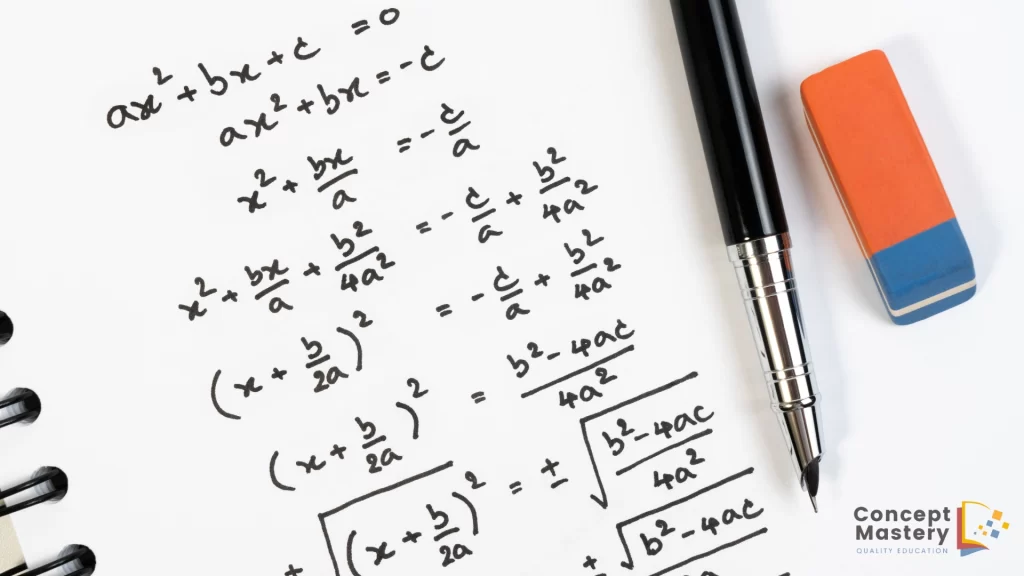
Understand the Problem:
Before diving into solving, take a moment to read the problem multiple times. Try rephrasing it in your own words. This ensures that you grasp the core of the challenge. Ask yourself: What is the problem really asking? What are the known quantities, and what are the unknowns?
Identify Knowns and Unknowns:
Listing out what you already know helps in structuring your thought process. If, for instance, you’re solving for ‘x’, recognize its role in the equation and how it relates to other quantities.
Break It Down:
Complex problems often become more manageable when divided into smaller, digestible parts. Try solving each part separately. This can lead to incremental victories that, when pieced together, solve the entire puzzle.
Visualize If Possible:
Sometimes, drawing a diagram or sketch can provide clarity. Whether it’s a word problem about distances, areas, or other scenarios, visual aids often provide insights that words alone cannot.
Use Resources and Tools:
There are various tools at your disposal—from calculators to algebraic software—that can assist in simplifying parts of the problem. Using them judiciously can save time and reduce potential errors.
Seek External Guidance:

No one said you have to face math challenges alone. When problems seem overly complicated, it’s wise to reach out for help. A Math tutor online can provide real-time feedback and strategies tailored to your unique learning style. For those who prefer face-to-face interaction, there are excellent in-person resources. If you’re located in the vicinity, consider reaching out to Math tutors in Oakville, who can offer personalized, hands-on instruction to clarify concepts and techniques.
Review and Double-Check:
Once you believe you’ve found a solution, revisit the original problem. Does your solution fit within the context provided? Double-checking ensures that you don’t overlook any nuances or make arithmetic errors.
Grasping algebraic concepts with clarity can be a game-changer for your academic journey. From better grades to a profound understanding of the world around you, mastering algebra paves the way. If you’re seeking personalized guidance tailored to your needs, reach out to Concept Mastery for Math tutoring online or explore options in your locality, like Math tutors in Oakville.
Remember, the right support can make algebra not just understandable but enjoyable!

